Community
The title “The Small Learning” refers to the part “Paragraph 7” of Cornelius Cardew’s piece “The Great Learning” (1971), a composition for vocal ensemble consisting of a set of rules that each musician should follow, leading to a kind of emergent harmony. “The Small Learning” also consists of an ensemble of acting sound generators or “agents’’ that all follow the same rules. In this case, there are five algorithmic systems that generate synthesized sounds, record ambient sounds, analyze them, and compare them to the synthesized sounds.
“The Small Learning” aims at the emergence of a sonic community, a form of ecology, that connects algorithmic processes, the sonic environment, and musical ideas. Density, pitch, timbre, and musical development emerge from the interactions of the various processes and agents, their materialities, and the ways in which they represent and transmit one another. The sound-generating agents are chaotic systems that, although very simply constructed, have a large space of possibility. It fascinates me aesthetically to experience and trace this space. Interaction with this system often results in surprising patterns, sudden transitions, and sound structures that change and dissolve. I am interested in how this complexity in the small and quasi-ideal domain of digital sound synthesis, can be connected to the sonic environment, i.e. how algorithmic chaos and the unpredictability of the external environment can encounter each other. This is done through a machine learning process that, in a sense, translates data and sounds into each other, adaptively adjusting sound synthesis to the results of an analysis of the environment.

Wavefolding
The sounds are generated using a feedback wavefolder. A wavefolder is a type of distortion device used especially in analog synthesizers. The general operation of a wavefolder can be described as folding, i.e. reflecting or inverting, an input signal as its magnitude exceeds a certain threshold in both the negative and positive ranges (see Figure 1). Additionally, the wave can still be shifted and thus asymmetric foldings can occur (see Figure 2 and Example 1). Here, I have transferred my experience with analog wavefolders to the digital domain. Wavefolders become especially interesting in feedback systems, because they can thus form an essential part of chaotic systems as a parameterized nonlinear function. Feedback wavefolders can produce both periodic and chaotic timbral states. The system used here, while very simple in its components (the feedback input wave is folded at certain thresholds), exhibits very diverse behavior that is difficult to understand.

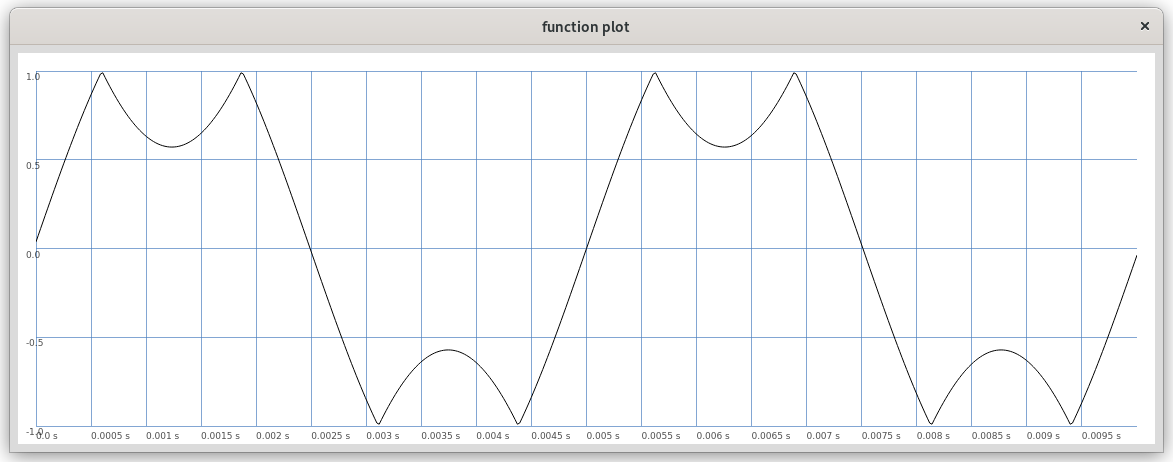
Figure 1: A sine wave folded at amplitude 0.7
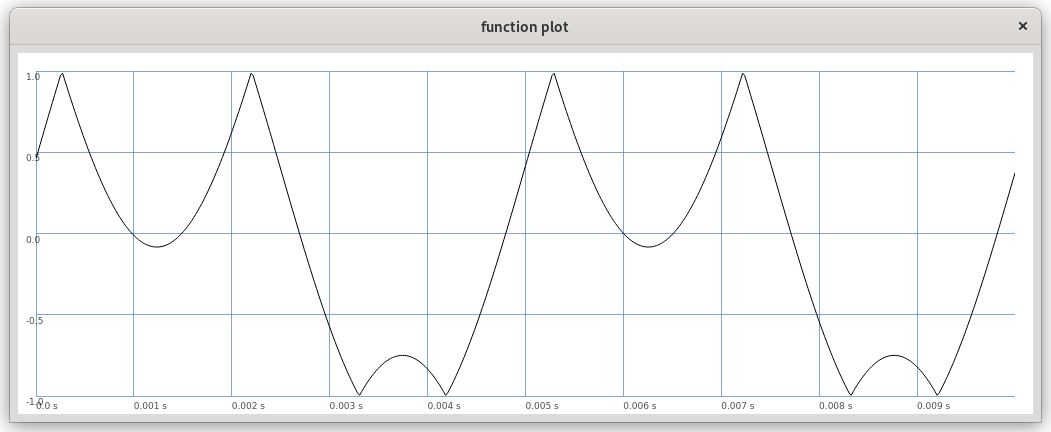
Figure 2: Asymmetric folding
|
( |
Example 1: Wavefolder with control of the threshold of the folding and the shift
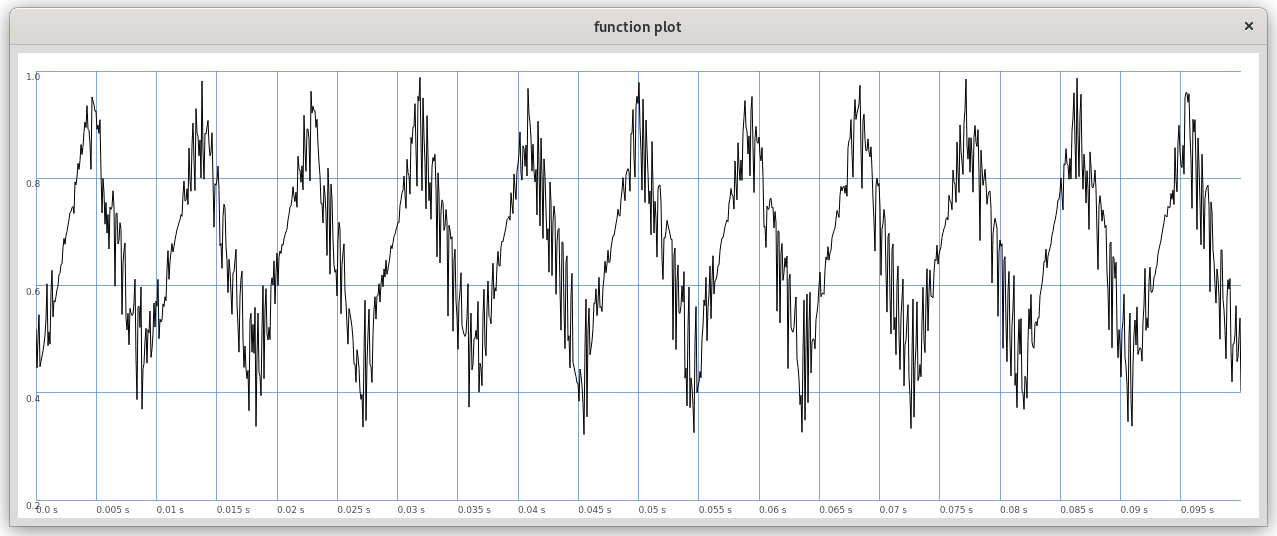
Figure 3: Feedback wavefolder (without external input) with quasi-periodic behavior
|
( |
Example 2: Wavefolder with feedback
Learning
Each of the five agents generates sounds using a feedback wavefolder and alternates between sound production and silence. Both their own sounds and ambient sounds picked up by the microphone during the silence phases are analyzed. Thus, playing and pausing alternate, with the analysis (or “listening”) directed inward and outward, respectively. The analysis produces mel-frequency cepstrum coefficients (MFCC)1 that are used for automatic speech recognition. The coefficients represent, with relatively little data (13 numbers in this case), essential properties of the frequency spectrum at one point in time.
After each iteration, the agents consider how close their generated sounds are to the environmental sounds they recorded and analyzed during their last pause, that is, how similar their respective MFCCs are. This is done using one of the simplest machine learning algorithms, the k-nearest neighbor (kNN)2 algorithm. The learning algorithm collects parameter values and analyses and generates new parameter values based on the collected data and a calculation of the distances between analysis data. The agents then use this algorithm to try to generate parameter values for themselves that approximate the environmental sounds, which of course include the sounds of the other agents. In this process, they also learn about their own chaotic behavior by learning to generate increasingly accurate parameter settings for specific timbres. The further they are sonically removed from the surrounding sounds, the more erratically they try to explore different possibilities. Once they are better adapted, their exploratory curiosity diminishes and they produce longer sounds. Thus, the rhythmic structures, musical density, and variability result from this adaptation process. In the process, they listen to each other and to the external environmental sounds, gather data and try to adapt, forming a sonic community with each other and with the environment.
Balancing
Here, the machine learning algorithm functions as a kind of counterforce that attempts to construct predictable relations between the chaotic behaviors and the unpredictable environmental sounds. Because of the multiple interfaces, such as microphone, analog-to-digital converter, MFCC analysis, parameter values, space, and loudspeakers, they will never succeed in predicting their own behavior or reproducing an external sound accurately. These interfaces act as reducing and distorting layers of representation and thus become productive. With the daily reboot, the existing data is erased and the process begins again.
Link to the GitLab repository
Get the code: https://gitlab.mur.at/pirro/klangnetze/-/tree/main/das_kleine_lernen