Gemeinschaft
Der Titel „Das kleine Lernen” bezieht sich auf den Teil „Paragraph 7” von Cornelius Cardews Stück „The Great Learning” (1971), eine Kompositionen für Vokalensemble, die aus einer Reihe von Regeln besteht, die jede:r Musiker:in befolgt und die zu einer Art emergenter Harmonie führen. „Das kleine Lernen” besteht ebenfalls aus einem Ensemble von handelnden Klangerzeugern oder „Agenten’’, die alle dieselben Regeln befolgen. In diesem Fall sind es fünf algorithmische Systeme, die synthetische Klänge erzeugen, Umgebungsklänge aufnehmen, analysieren und mit den synthetisierten Klängen vergleichen.
„Das kleine Lernen” hat es zum Ziel, eine klangliche Gemeinschaft, eine Form von Ökologie, entstehen zu lassen, die algorithmische Prozesse, die klangliche Umwelt und musikalische Ideen miteinander verbindet. Dichte, Tonhöhen, Klangfarben und musikalische Entwicklungen entstehen dabei aus den Interaktionen der verschiedenen Prozesse und Agenten, ihren Materialitäten und der Art und Weise, wie sie einander repräsentieren und übertragen. Die klangerzeugenden Agenten sind chaotische Systeme, die — obwohl sie sehr einfach aufgebaut sind — einen großen Möglichkeitsraum haben. Es fasziniert mich ästhetisch, diesen Raum zu erfahren und nachzuvollziehen. So kommt es in der Interaktion mit diesem System oft zu überraschenden Muster, plötzlichen Übergängen, und Klangstrukturen, die sich verändern und auflösen. Mich interessiert, wie diese Komplexität in einem kleinen und quasi-ideellen Bereich der digitalen Klangsynthese mit der klanglichen Umwelt verbunden werden kann, d.h. wie sich algorithmisches Chaos und die Unvorhersehbarkeit der äußeren Umwelt begegnen können. Dies geschieht durch einen maschinellen Lernprozess, der gewissermaßen Daten und Klänge ineinander übersetzt und somit die Klangsynthese adaptiv an eine Analyse der Umwelt anpasst.

Wavefolding
Die Klänge werden mit einem rückgekoppelten Wavefolder erzeugt. Ein Wavefolder ist eine Art von Verzerrer, der besonders in analogen Synthesizern verwendet wird. Die allgemeine Funktionsweise eines Wavefolders kann so beschrieben werden, dass ein Eingangssignal bei zunehmender Größe an einer gewissen Schwelle sowohl im negativen als auch im positiven Bereich gefaltet, also reflektiert oder invertiert wird (siehe Abbildung 1). Dabei kann die Welle noch verschoben werden und so können asymmetrische Faltungen entstehen (siehe Abbildung 2 und Beispiel 1). Ich habe hier meine Erfahrungen mit analogen Wavefoldern in den digitalen Bereich übertragen. Besonders interessant werden Wavefolder in Feedback-Systemen, da sie somit als parametrisierte nichtlineare Funktion einen wesentlichen Teil chaotischer Systeme bilden können. Rückgekoppelte Wavefolder können sowohl periodische als auch chaotische klangliche Zustände erzeugen. Das System, das hier verwendet wird, ist zwar in seinen Bestandteilen sehr einfach (die rückgekoppelte Eingangswelle wird an bestimmten Schwellen gefaltet), zeigt aber ein schwer verauszusehendes und vielfältiges Verhalten.

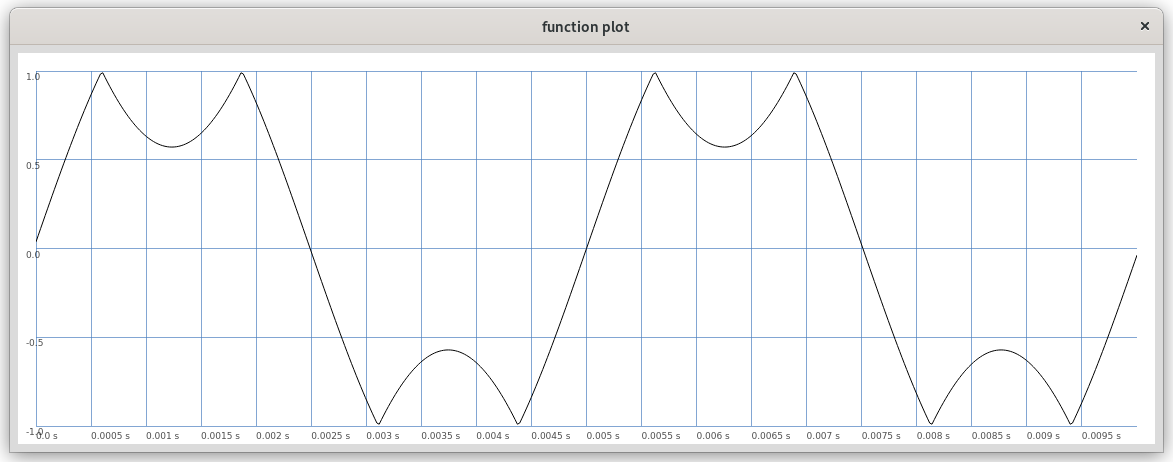
Abbildung 1: Eine Sinuswelle, die bei Amplitude 0.7 gefaltet wird
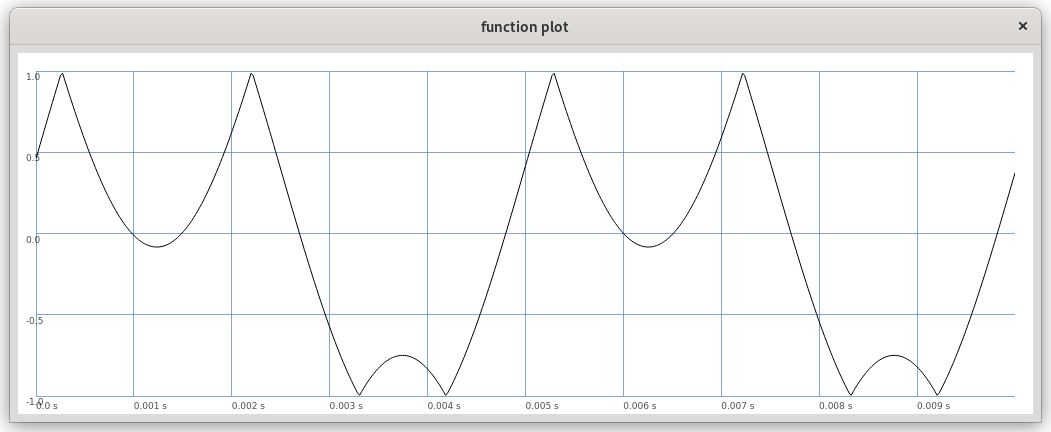
Abbildung 2: Asymmetrische Faltung
|
( |
Beispiel 1: Wavefolder mit Steuerung der Schwelle der Faltung und der Verschiebung (shift)
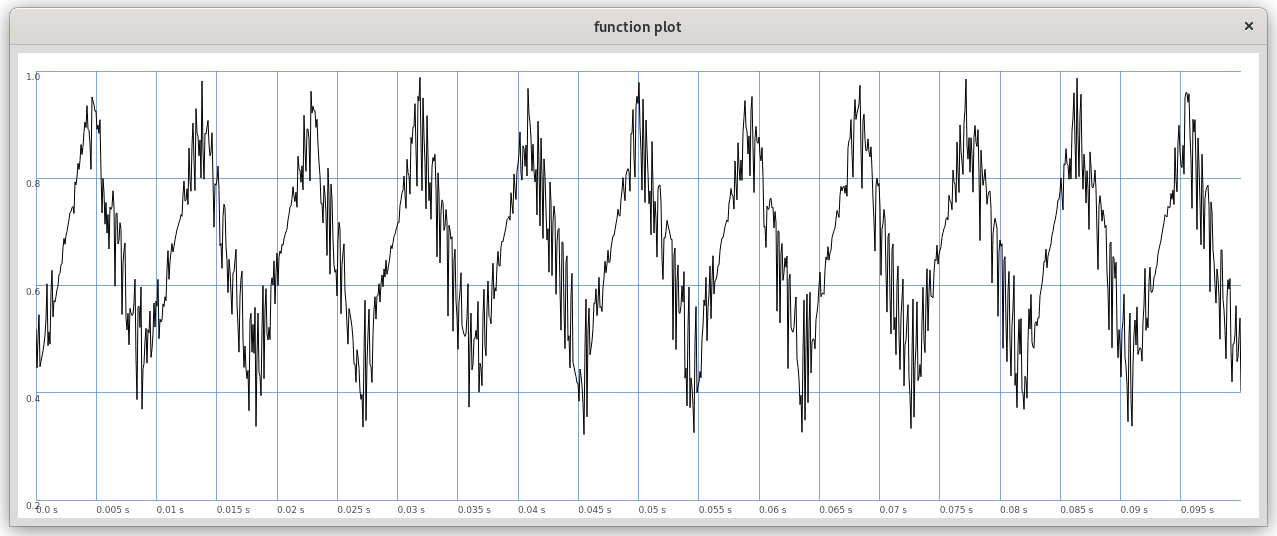
Abbildung 3: Rückgekoppelter Wavefolder (ohne externen Input) mit quasi-periodischem Verhalten
|
( |
Beispiel 2: Rückgekoppelter Wavefolder
Lernen
Jeder der fünf Agenten generiert Klänge mithilfe von jeweils einem rückgekoppelten Wavefolder und wechselt zwischen Klangproduktion und Stille. Sowohl die eigenen Klänge als auch Umgebungsgeräusche, die während der Stille-Phasen durch das Mikrofon aufgenommen werden, werden analysiert. So wechseln sich Spielen und Pausieren ab, wobei die Analyse (oder das „Hören”) jeweils nach Innen beziehungsweise nach Außen gerichtet ist. Die Analyse erzeugt Mel-Frequenz-Cepstrum-Koeffizienten (MFCC)1, die zur automatischen Spracherkennung verwendet werden. Die Koeffizienten stellen mit relativ wenig Daten (13 Zahlen in diesem Fall) wesentliche Eigenschaften des Frequenzspektrums zu einem Zeitpunkt dar.
Nach jeder Iteration gleichen die Agenten ab, wie nahe ihre erzeugten Klänge an den Umweltklängen sind, die sie während ihrer letzten Pause aufgenommen und analysiert haben, das heißt wie ähnlich sich die jeweiligen MFCCs sind. Dabei wird einer der einfachsten maschinellen Lernalgorithmen verwendet, der k-nächste-Nachbarn-Algorithmus (kNN)2. Der Lernalgorithmus sammelt Parameterwerte und Analysedaten und erzeugt neue Parameterwerte auf Grundlage der gesammelten Daten und einer Berechnung der Abstände von Analysedaten zueinander. Die Agenten versuchen dann mithilfe dieses Algorithmus, Parameterwerte für sich selbst zu erzeugen, die der Umweltklänge nahekommen, welche natürlich wesentlich auch die Klänge der anderen Agenten beinhalten. In diesem Prozess lernen sie auch ihr eigenes chaotisches Verhalten kennen, indem sie immer genauere Parameter-Settings für bestimmte Klangfarben erzeugen lernen. Je weiter sie klanglich von den Umgebungsklängen entfernt sind, desto erratischer versuchen sie verschiedene Möglichkeiten zu erkunden. Sobald sie besser adaptiert sind, verringert sich ihre explorative Neugier und sie erzeugen längere Klänge. Die rhythmischen Strukturen, die musikalische Dichte und Variabilität ergibt sich also aus diesem Adaptionsprozess. Sie hören dabei sich gegenseitig und den äußeren Umgebungsklängen zu, sammeln Daten und versuchen sich zu adaptieren, bilden eine klangliche Gemeinschaft untereinander und mit der Umwelt.
Balanzieren
Der maschinelle Lernalgorithmus funktioniert hier als eine Art Gegenkraft, die versucht, die chaotischen Verhaltensweisen und die unvorhersehbaren Umweltklänge in einen vorhersagbaren Bezug zu bringen. Durch die mehrfachen Schnittstellen, wie Mikrofon, Analog-Digital-Konverter, MFCC-Analyse, Parameterwerte, Raum und Lautsprecher, wird es ihnen nie gelingen, ihr eigenes Verhalten vorhersagen zu können oder einen äußeren Klang genau zu reproduzieren. Diese Schnittstellen agieren als reduzierenden und verzerrende Repräsentationschichten und werden somit produktiv. Mit dem täglichen Neustart werden die vorhandenen Daten gelöscht und der Vorgang beginnt von Neuem.
Link zum GitLab Repository
Code herunterladen: https://gitlab.mur.at/pirro/klangnetze/-/tree/main/das_kleine_lernen